本研究的目的是找到一个稳定的频谱特征,并说明该特征在压缩原始信号中的可用性。压缩方法适用于振动触觉加速度,不适用于力和速度数据。因为力和速度信号的功率都集中在一个很低的频率范围内,所以很难区分趋势是否一致。此外,基于STFT频谱特性的方法可以进一步降低压缩比,用于长期数据压缩和多交互点的应用。所提出的编码和解码方案是基于频域的。得到归一化幅度谱即可重构原始波形,STFT幅度谱在每个时间窗内的最大值,和少量的初始阶段。对于相同材质的表面纹理,虽然用量
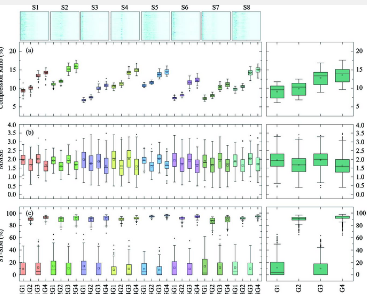
随着数据采集时间的延长,数据显着增加,或者随着采集点数量的增加,压缩后的数据增加量仍然很小;即,压缩比变小。这是因为无论数据如何增加,归一化幅度谱特性变化不大,压缩后的数据增加量很小。最后,虽然我们在日常生活中遇到的大多数材料的表面纹理都是近似各向同性和均匀的,但我们必须讨论所提出的解决方案在表面各向异性或不平坦的情况下的适用性:
• 如果每单位周期的实际变化率小于某个临界值,表面仍被认为是均匀和各向同性的。触觉数据的短期振幅谱趋势在过滤后保持相似。
• 表面在一个小的时间窗内均匀且各向同性,或者表面纹理的变化并不剧烈,无论是否能被感知,本研究中的方法仍然适用。STFT归一化频谱特性采用JPEG标准进行压缩,对于平滑变化的图像仍能达到较高的压缩比。
• 特别是,如果将两种材料的纹理拼接在一起,则证明了频域压缩的优势。如果两种材料的纹理光谱特征相似,则无需处理。否则很容易通过归一化后的频谱图找到两个不同频谱分布的分界点,然后分别进行压缩。
另外,考虑到本研究是基于STFT的,需要将一个时间窗的数据看成一个帧。数据压缩是没有问题的,但是如果需要实时压缩,也就是减少数据帧的长度,这个谱特征的稳定性就会下降,压缩效率也会变差。这也是之前选择500ms数据进行处理的原因。
作者发现同类表面纹理振动触觉加速度的STFT谱具有较高的相似度,并利用这种相似性对振动触觉加速度与公开数据库进行编码,实现了10%的压缩。同时,用于重构原始信号的改进G&L算法实现了至少90%的时频相似性。发现原始信号和恢复信号之间相似性的主观得分很高,平均为 87.85。对于空间中的多交互点,可以复用趋势相似度灰度图,进一步降低压缩率。

